Topological quantum codes

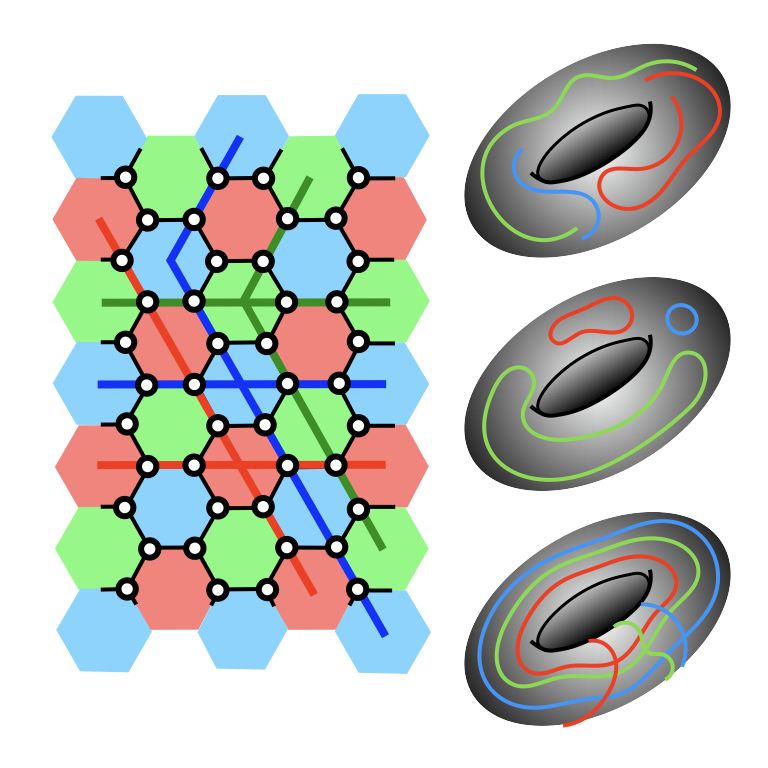Topological quantum error correcting codes, including the Kitaev code and the color code, have emerged as leading candidates towards the goal of achieving large-scale fault-tolerant quantum computers. These systems are realized by arranging qubits on lattices of specific geometry, and are robust against external perturbation, qubit loss, and computational errors. These systems have also been implemented in the laboratory with, for example, trapped ions, and superconducting qubits. It is now clear that in order to host a single logical qubit with low or moderate code distance, and to perform error correction protocols taking into account errors on multiple physical qubits, one needs to deal with systems with a large number of physical qubits in the presence of noise. This makes the investigation of these systems difficult both in the theoretical and experimental fronts. Our research aims to explore two directions: (1) effect of external perturbations such as local magnetic fields, spin-spin interactions, and disorder in these systems, and (2) characterization of these systems using entanglement measures in an experimentally realistic way.